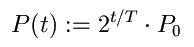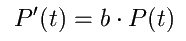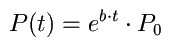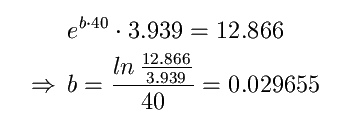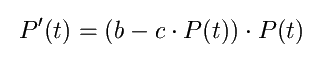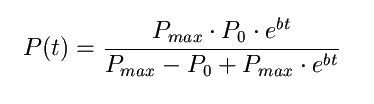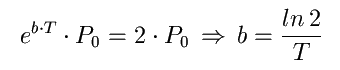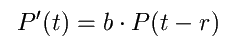Anwendung der Exponentialfunktion in der Biologie
anhand ausgewählter Beispiele
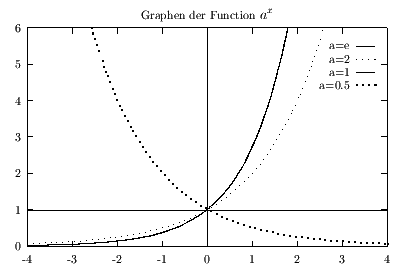
Unter Exponentialfunktionen versteht man Funktionen des Typs
y=ax. a heißt Basis und x Exponent [3].
x ist hierbei aus der Menge der reellen Zahlen, a ist
größer 0. Die Funktion ist monoton wachsend, für a größer
1. Für 0 kleiner a kleiner 1 ist sie monoton fallend; für a=1
ist sie konstant.
Eine Besondere Eigenschaft der Exponentialfunktion ist es, daß
ihr Zuwachs bzw. ihre Steigung proportional zu ihrem Betrag ist. Ist
die Basis die eulersche Zahl e (=2.71828...) [3] so sind Betrag und
Steigung der Funktion ex überall gleich
dem Funktionswert.
Wachstum, wie es in dieser Darstellung auftritt, behandelt die Zunahme der
Population, d.h. die Vergrößerung der Anzahl der einzelnen Lebewesen.
Diese Zunahme wird entweder durch Zellteilung oder Geburten bedingt.
Das Wachstum wird in der Geburtenrate dargelegt.
Jeder zellbiologische Teilungsprozess hat eine bestimmte Generationsdauer.
Darunter versteht man die Zeit von einer Zellteilung zur nächsten.
Bei jedem Teilungsprozess
verdoppelt sich der Zellbestand. Dieser kann folglich mit 2 hoch Nummer der
Generation bestimmt werden. Die Generationsnummer ergibt sich näherungsweise
aus der
seit Beginn der Betrachtung vergangen Zeit und der Generationsdauer, in dem
die vergangene Zeit durch die Generationsdauer teilt.
| P(t) |
ist die Größe der Population zum Zeitpunkt t |
| P0 |
ist die Größe der Population zu Beginn der Betrachtung |
| t |
ist die Zeit seit Beobachtungsbeginn |
| T |
ist die Generationsdauer |
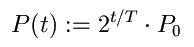Die betrachteten Bakterien heißen Bacillus cereus, Bacillus subtilis
und Serratia marcescens. Die Generationsdauern betragen
18.8 Min (bei 37C), 35 Min (36C) und
28 Min (35C) [1].
Den Verlauf des Wachstums kann man folgender Grafik entnehmen.
Beginnt das Wachstum mit einer Zelle so verlaufen die nachfolgenden
Teilungen im ``Gleichtakt''.
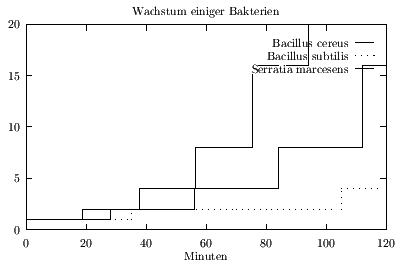
Im folgenden wird das Wachstum von verschiedenen Protozoen der
Gattungen Amoeba vespertilio, Paramecium aurelia und Pelomyxa binucleata.
Die Teilungsdauer dieser Gattungen beträgt 1 Std, 2 Std und 7.5 Std.
Zum Zeitpunkt Null sind von jeder Gattung hundert Exemplare vorhanden.
[1]
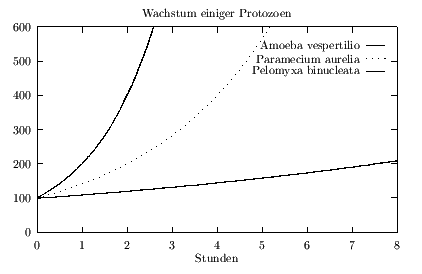
Beim klassischen Wachstum geht man von folgenden Bedingungen aus [4]:
- es steht immer genug Lebensraum zur Verfügung
- die Versorgung mit überlebensrelevanten Nährstoffen ist nicht
begrenzt
- alle betrachteten Lebewesen existieren mindestens für den Zeitraum
der Betrachtung
- die Geburtenrate, d.h. der relative Zuwachs, ist für den Zeitraum
der Betrachtung konstant
Der Zuwachs der Population entspricht der Ableitung der Populationskurve
zu einem bestimmten Zeitpunkt. Der Zuwachs ist unter den genannten
Bedingungen proportional zum Bestand. Die Proportionalitätskonstante ist
hierbei genau die Geburtenrate [4]. Es gilt:
| P'(t) |
ist die Ableitung der Funktion P(t) |
| b |
ist die Geburtenrate (b > 0) |
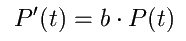
Als Lösung für die oben genannte Gleichung wird in der Literatur
folgendes angegeben[4]:
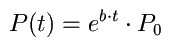
Als Beispiel wird diesmal das Wachstum der amerikanischen Bevölkerung
gewählt. Aus den Volkszählungen sind unten genannte Zahlen bekannt [4].
Mittels der Exponentialfunktion soll versucht werden von den frühen
Jahren auf die Population in den späten zu schließen.
| Jahr |
Population in Millionen |
| 1790 |
3.939 |
| 1800 |
5.308 |
| 1810 |
7.24 |
| 1820 |
9.638 |
| 1830 |
12.866 |
| 1840 |
17.069 |
| 1850 |
23.192 |
| 1860 |
31.443 |
| 1870 |
38.558 |
| 1880 |
50.156 |
| 1890 |
62.948 |
| 1900 |
75.995 |
| 1970 |
203.185 |
P0 beträgt offenbar 3.939
Als zweiten Zeitpunkt betrachte man das Jahr 1830.
Die Zeit seit Betrachtungsbeginn ist hier 40 Jahre:
P(40) = 12.866
Die Wachstumsrate errechnet sich folgendermaßen:
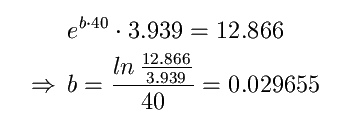
In der folgenden Grafik kann man die tatsächlichen Werte mit der
berechneten Kurve vergleichen. Man sieht, daß bis zum Jahre 1860, also
über 30 Jahre lang, die Prognose sehr exakt ist. Danach wird
sie jedoch unbrauchbar. Für das Jahr 1970 würde eine Population
von exp(0.0297*180) * 3.939 = 819.6, also ein vierfacher
Wert.
Bei längerfristiger Betrachtung wird das Anfangs exponentielle
Wachstum durch das begrenzte Nahrungs- und Platzangebot begrenzt.
In der Praxis hat es sich als sinnvoll erwiesen die Geburtenrate
in Abhängigkeit der Population zu setzten. Die so korrigierte
Wachstumsrate soll Null sein, wenn die maximale Größe der Bevölkerung
erreicht ist, und soll gleich der ursprünglichen Geburtenrate bei
niedriger Populationsgröße sein [4].
| Pmax |
maximale Bevölkerungsgröße |
| c |
Korrekturfaktor: b-c * Pmax = 0 |
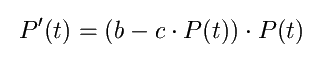
Die Verhulst-Pearlsche Gleichung lautet [2]:
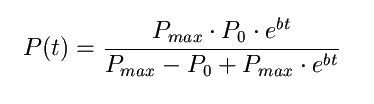
Man betrachtet die bereits in 2.1.3 besprochenen Protozoen der
Gattungen Amoeba vespertilio, Paramecium aurelia und Pelomyxa binucleata.
Aus den Generationsdauern (1 Std, 2 Std und 7.5 Std [1]) müssen die
Wachstumsrate pro Stunde berechnet werden, um sie in die Gleichung
einsetzen zu können.
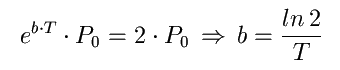
| bAmoeba |
= |
0.6931471 |
| bParamecium |
= |
0.3465735 |
| bPelomyxa |
= |
0.0924196 |
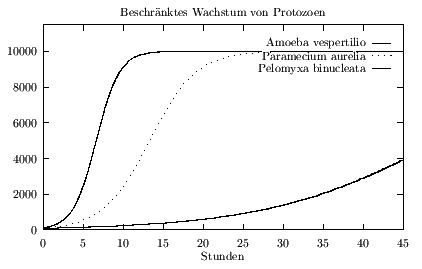
Die Einzeller befinden sich in Gefäßen in denen Nahrung für
10000 ihrer Art zur Verfügung gestellt wird.
Zu Beginn der Betrachtung werden je 100 Wesen in ein Gefäß
gesetzt.
Bei vielen Tieren besteht eine Zeitdifferenz zwischen Geburt und
Geschlechtsreife. Dies kann man beim erstellen der Formel berücksichtigen,
indem man die Geburtenrate nicht auf den Gesamtbestand, sondern nur auf
den geschlechtsreifen Teil bezieht. Da in dem Modell keine Tiere sterben,
entspricht dem geschlechtsreifen Teil der Population zum Zeitpunkt t
genau die Größe der Population zum Zeitpunkt t-r, wobei r die Reifezeit
ist. [2]
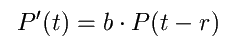
Diese Gleichung ist der ursprünglichen sehr ähnlich,
läßt sich aber nur schwer in verständliche und
anwendbare Form bringen.
Wie ich in der Ausführung gezeigt habe, erweist sich das mathematische
Modell als sehr Leistungsfähig, was die Vorhersage von Populationsgrößen
betrifft. Die Exponentialfunktion fand Anwendung bei: Verdoppelung in konstanten
Zeitintervallen, Wachstum mit konstanter Geburtenrate, Wachstum bei
festgelegter Maximalbevölkerung. Ein häufiger Ansatz zur Ermittlung dieser
Gleichungen ist es, den Bevölkerungszuwachs mit der aktuellen Bevölkerung
in Beziehung zu setzten. Dieses Verfahren wird in der Mathematik als
Differentialgleichung bezeichnet. Die einzelnen Schritte zur Lösung konnten
leider, nicht zu letzt mangels eigenen Wissens, von mir nicht im einzelnen
nachvollzogen und dargelegt werden. Aber ich hoffe, ich konnte doch
die wichtigsten Überlegungen, die zur Formel führten,
anschaulich darstellen.
Die hier von mir erläuterten Beispiele lassen auf den ersten Blick darauf
schließen, daß sich biologische Vorgänge problemlos in mathematischen
Formeln darstellen lassen. Die Schwierigkeit besteht jedoch darin, die
in dieser Ausführung stets relevanten Einschränkungen in der Natur
ausschließen zu können. Die streng exponentielle Vermehrung von
Protozoen zum Beispiel findet in der genannten Form, wegen der zahlreichen
Störungen, wie z.B. Temperaturschwankungen, schwankendes Nahrungsangebot,
genetische Aberrationen und Einflüsse durch andere Lebewesen, nicht statt.
| [1] |
Rainer Flindt |
| |
Biologie in Zahlen |
| |
4.Auflage, Stuttgart, 1995 |
| [2] |
Nöbauer/ Timischl |
| |
Mathematische Modelle in der Biologie |
| |
Braunschweig, 1979 |
| [3] |
Bearbeitet von Prof. Dr. Scheid |
| |
Duden Rechenen und Mathematik, 1985 |
| [4] |
``The Growth of Population'' |
| |
http://www.dept.physics.upenn.edu/courses/gladney/ |
| |
mathphys/subsection2 1 2 |