Dadim propaganda page

What is Dadim

Dadim stems from da, the mandarin pronunciation of meaning big, and dim which is short for dimension. Dadim is a computational representation of high dimensional functions. It is based on sparse grids, which were found by Smolyak to store high dimensional data efficiently. Sparse grids have since been further developed by Zenger and Griebel. Various implementations showed the computational power and were often said to overcome the so called "curse of dimension". It can therefore extend many well known techniques, like wavelets and finite elements, to problems which can today only be treated by random grids or Monte Carlo methods. Dadim comes along with an implementation of several mathematical operators which allow for differential analysis, solution of partial differential equations and data compression. High dimensional analysis can be employed in a wide range scientific disciplines. Below there are some examples for an application in financial modeling.

Historical data analysis and model fitting

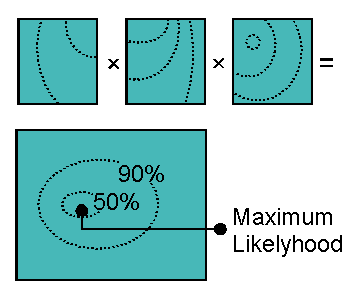
It is typically easier to introduce new parameters to a mathematical model, than to associate any market meaning with it or even to derive a specific value for it. Any additional degree of freedom increases the complexity of traditional algorithms exponentially. With Dadim it is possible to solve this high dimensional problem numerically and makes it more or less trivial to formulate the mathematical model and to compute a confidence interval together with a maximum likelihood estimate.

Example 1: GARCH vola fitting

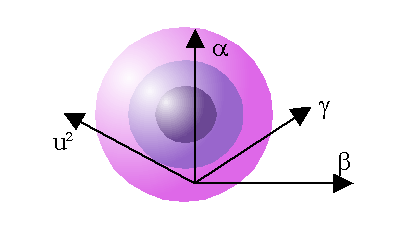
The GARCH model computes for three parameters alpha, beta, gamma and a given history of price jumps a volatility estimate, which is nothing else but a probability distribution of u, the succeeding price jump.
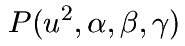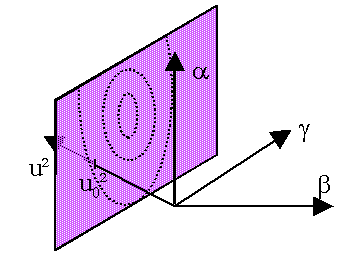
	At a certain time t0 there occurs a price jump u0. This leads to probability distribution of the three GARCH parameters.
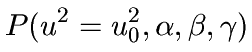Assuming independence of all price jump samples, one can obtain the joint distribution by multiplying all individual distributions for different times ti

Data extrapolation

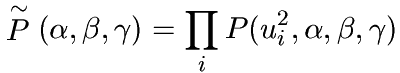Numerical tasks often involve inter- and extrapolation of data samples. Since there rarely is a mathematically unique solution, one wishes to have tight control over the algorithms outcome and an intuitive configuration interface. Defining and solving a PDE associated with this problem has several advantages:

• well defined, mathematically
  PDEs and their solution are well understood and many of their properties can be formulated exactly.
• Intuitive
  Due to their tight relation to physical problems, their behavior and their reaction to parameter variation can be comprehended easily.
• Compatible
  There are several PDE solvers as well as tools for analyzing and designing PDEs. All of them share the common mathematical notation.

Example 2: Vola surface interpolation

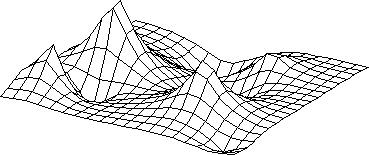
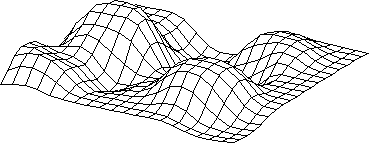
One of the most simple PDE is the Laplace equation, modeling a trampoline being elevated at certain points.
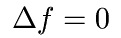	In order to avoid singularities at the sample points one can introduce additional smoothness by considering the functions gradient.
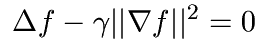Not feeling comfortable with the mathematical notation, one can use an XML editor featuring a tree structure and a more specific naming for different portions of an equation.

Pricing exotic derivatives

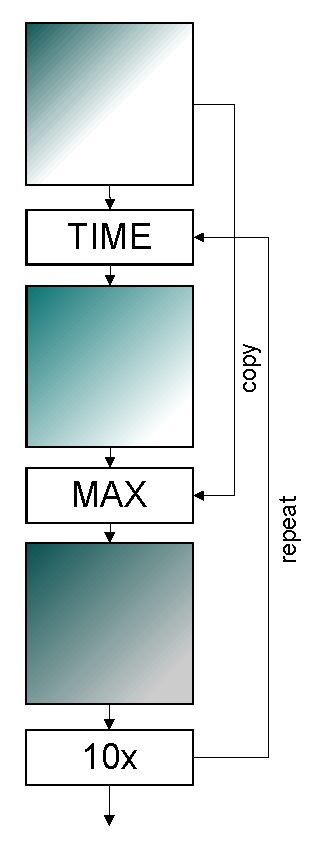
Nowadays, everyone can price exotic derivatives. So can Dadim. The goal of a PDE solver is to maximize computational speed, while keeping the pricing as configurable and open as possible. PDEs are capable of describing all kinds of Markov processes. Therefore they can easily be used for tasks done Monte Carlo or binomial tree implementations. The advantages of Dadim are higher speed, straight forward model fitting and unlimited configurability of the underlying formulas.

Example 3: Pricing an American spread option

Let the initial payoff structure be defined as max(S1-S2, 0). It can be visualized in a plane with an S1- and S2-axis and a color representing the option's present value. As time passes a diffusion and convection process models the stochastic price movements and the discounting. The diffusion can be computed by a convolution with an arbitrary joint distribution, such that any stochastic process can be incorporated. After discrete time intervals, one has the option of immediate execution and further keeping. For all stock prices the value of this option is chosen as the maximum between the original payoff and the current value of the convection-diffusion process. Finally, the diffusion and maximizing steps can be repeated for the number of time steps to option maturity.