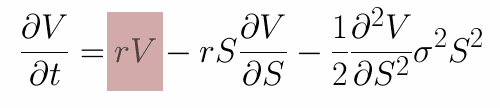
 click to proceed to the next image |
Convection Diffusion Process in 1 dimension |
|---|
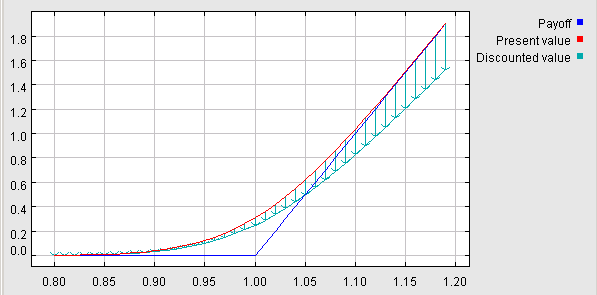
The image below shows how the theoretically computed option price changes when moving backward in time. As described by the Black-Scholes Equation, this process is governed by three different operators: Scale, Shift and Blur. The Blur operator (Diffusion) smoothens the function by averaging the values of different possible underlying prices according to their probabilities. The shift operator (Convection) models the underlyings drift by copying a value to the position determined by the drift's speed.
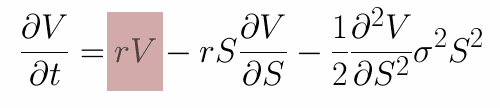
 click to proceed to the next image |
Blur operator |
|
|---|---|
| The Blur operator models a diffusion process, which in turn is determined by a probability distribution of parameter changes. The animation shows how an images is affected by a diffusion process with two correlated dimensions. The correlation yields a much faster smothening in the (1,1) direction, where both parameters change by the same amount. Only little diffusion occurs where parameters move in opposite directions (1, -1). | |
Definition:B f(x) = Integral f(x)P(x-s)dsApplications:
|  |
Shift operator | |
|---|---|
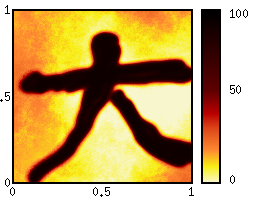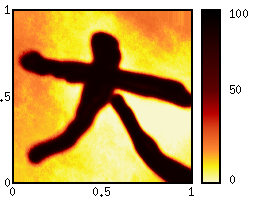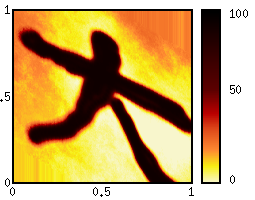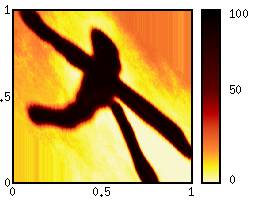
| The animation shows a shift process where the drift's speed is defined by the x-coordinate and the drift direction is along the y-axis. This makes it possible to implement discount processes with variable factors. Another important application is a summation step in Asian derivatives. Here the value of the new function is determined by the value of the old function where the y-coordinate is increased by x. | |
Definition:S f (x,y) = f (y + x, y)or, on a logarithmic scale S f (x, y) = f (y*(1+x), y) Applications:
|  |
Maximum operator | |
|---|---|
|
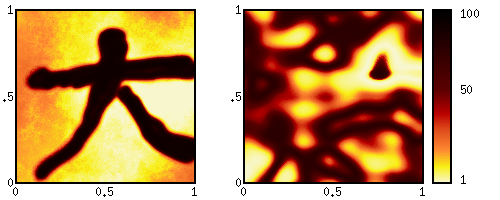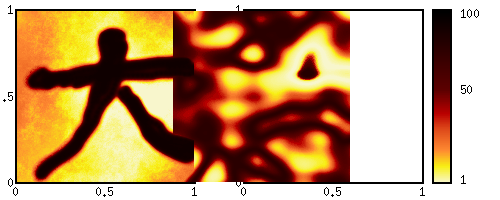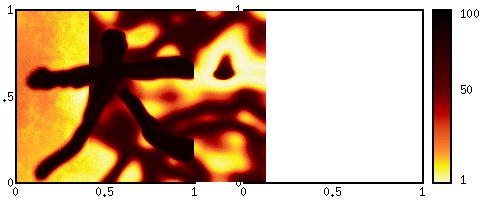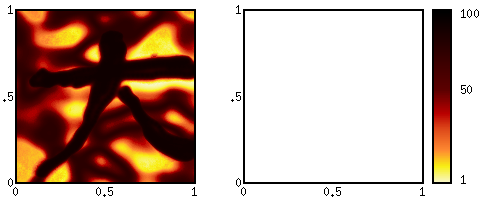
The maximum operator takes two functions and returns a single function
which is greater than each individual function. Consider the two
original functions to be the expected payoff of two investment
strategies. The maximized function represents the present value of
having the option between those two. An important application is an
American option where the choice of immediate excercising is exists in
every time step.
M A B (x, y) = max { A(x,y), B(x,y) } | |
| |
Exotic derivatives | |
|---|---|
Example: Pricing an Asian binary call
| 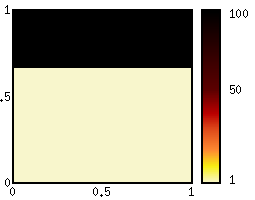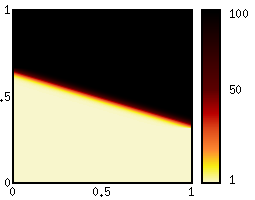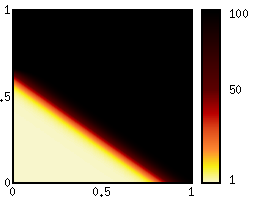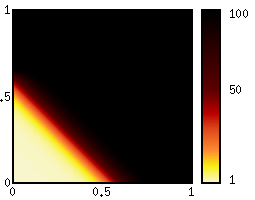 |
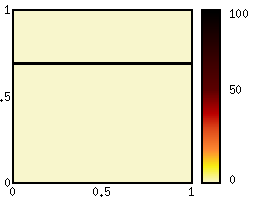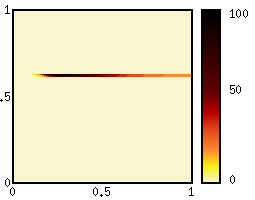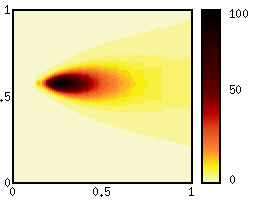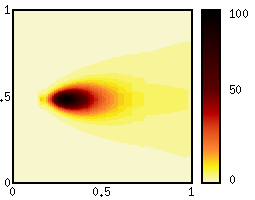
Modell fitting | |
|---|---|
Example: Volatility estimation
|  |
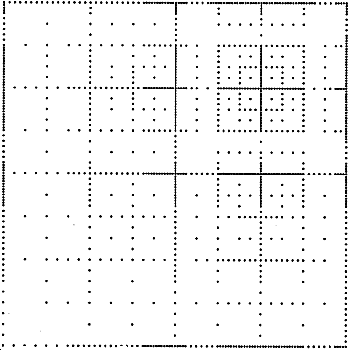
Efficient data structures | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Sparse GridsSprase grids store data points only at certain positions which where proved to allow optimal function reconstruction. Further improved adaptive data structures can exploit a posteriori results for eliminating further points.
|  | ||||||||||||
Dadim-XML: Storing operator trees | |
|---|---|
Dadim-XMLThe final goal is to find approximations for several kinds of functional operators by only using a small set of strongly optimized implementations. Dadim-XML identifies the types of operators and their possible combinations which maximize computational capability while keeping an intuitive and consistent mathematical framework. |
<Dadim>
<Binary underlying="S">
<Shift underlying="S" length="strike"/>
<Loop count="10">
<Shift underlying="S" target="sum"/>
<GaussianBlur underlying="S" deviation="volatility"/>
</Loop>
<Project underlying="sum" value="0"/>
<Project underlying="strike" value="100"/>
</Dadim>
|
Stefan Dirnstorfer